The definition of dimensions gives us a clearer view of the database structure.

The following is our familiar Entity-Relationship (E-R) diagram:

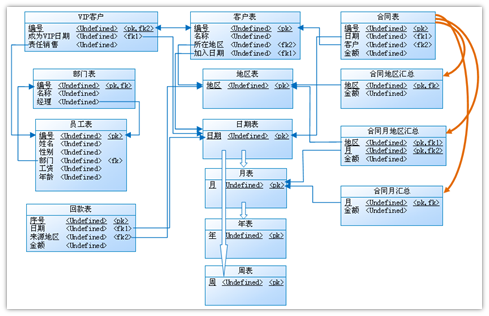
It is a net structure. The foreign key relationships between entities (tables) are drawn directly on the diagram. When there are a lot of entities, the diagram looks messy with lines spread in every direction because any two entities could have an associative relationship. The data structure is tightly coupled. When adding or deleting an entity, we need to take care of all the entities with which it associates. It is very likely that we miss an associative relationship or create a two-way connection.

With dimensions abstracted from the database structure, we can connect tables to them in a bus-based network:

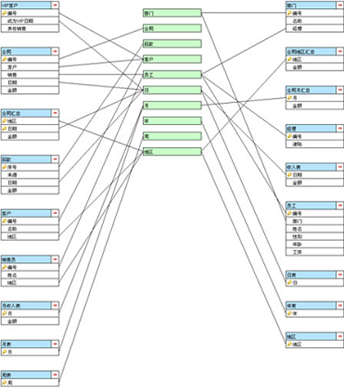
All the dimensions are listed in the center of the data structure. The entities (tables) are connected to the dimensions instead of to each other, creating a loosely coupled data structure. Adding or deleting an entity won’t affect other entities and there won’t be any omission or re-connection.

One thing we need to know is that, if drawn correctly, the number of associative lines in an E-R diagram and that in a bus-based network are nearly the same. This is because the number of lines is determined by the data associative relationships. Though the associative lines in a bus-based network are not less than those in an E-R diagram, the former shows the data structure in a clearer way.

In an effort to provide associative query ability, some BI products allow non-IT employees to view the associative relationships between tables (which is a part of the E-R diagram). The solution is basically impractical because they find it difficult to understand the diagram. There should be a practical solution that enables the non-IT employees to get a proper associative relationship intelligently according to their selected data items (fields).  

With the concept of dimensions, this goal can be achieved to some extent.  

After fields arearbitrarily selected, the tables where these fields are located, homo-dimension fields between these tables (primary key fieldsare preferred) are looked for, and a JOIN relationship is established based on the homo-dimension fields. When only one field ina table andthe primary key field of another table havethe same dimension, in most cases the JOIN relationship established based on these two fields is correct. In reality, when the data structure is not particularly complex, this condition can usually be met andcorrect association can really be automatically established based on the selected data items. Some BI products do make it.

But with SQL syntax, this approach cannot deal with a table’sself-association and the existence of multiple homo-dimensionfields between tables and multiple recursive associations. It is the DQL syntax that cansolve the association issues at the root.

As previously said, homo-dimension fields will be JOINed. That’s what the DQL syntax does.As long as fields (including general fields) are homo-dimension, they can be JOINed. But does such a JOIN always have business significance?

The answer is yes.JOINs between homo-dimension fieldsalways have value in business. In turn, fields to be JOINed must behomo-dimension;otherwise, the JOIN will be meaningless.But, JOINs between non-homo-dimension fields are not prohibited in SQL, as long as the fields have the same data type. That the associative fields in two tables are homo-dimension means a JOIN between them is meaningful. DQL ensures that tables are JOINed over homo-dimension fields.

The GROUP BY clause in DQL always corresponds to the ON clause (for a single table,the query can be regarded as one with the ON clause omitted). That is to say, GROUP BY is always performed overa certain dimension. This reflects the fact that group operationsover measuresare meaningless. As SQLdoes not define the concepts of dimension and measure, it does not prohibit operations over measures. DQL, by contrast,ensures that each group operation is meaningful in business.

Thiscan improve the performance of groupoperations. The rangeof values ofa dimension attributeisdetermined by the length of the dimension table. Since adimension table is always known in advance,we can use a method similar to radix sort algorithm to speed up the performance. This method can also be used to perform a sortingover adimension. Sincethe algorithm isless relevant to our topic, wewill not go into the details.