How to make the columnar storage data warehouse more efficient
Many data warehouses adopt the columnar storage. If the total number of columns in the data table is large and the number of columns involved in calculation is small, it only needs to read the desired columns when the columnar storage is used, which can reduce the access amount to hard disk, and improve the performance. Especially when the amount of data is very large, and the time to scan and read the hard disk accounts for a large proportion, the advantages of columnar storage will be obvious.
So, can we conclude that the best performance can be achieved as long as the columnar storage is used? Let’s see in which aspects can the columnar storage perform more efficiently.
Compression
The encoding method for structured data is generally not very compact, and there is often some space for compression. Usually, the data warehouse compresses the data based on columnar storage to physically reduce the data storage amount, so as to reduce the reading time and improve the performance. The data types of the same field in the data table are generally the same, and even the values are very close in some cases. For such a batch of data, a good compression rate can be obtained in general. Columnar storage is to store the values of the same field together, and hence it is more suitable for data compression than row-based storage.
However, the general compression algorithm cannot assume that the data has certain characteristics, and can only treat them as the free bytes stream to encode, and sometimes a best compression rate cannot be obtained. Moreover, the data compressed by the algorithm with high compression rate will often increase the operation amount of CPU and consume more time when decompressing, and the time increased in decompressing is even greater than the saved reading time of hard disk from data compression. As a result, the loss outweighs the gain.
If we process the data in advance to artificially make them have certain characteristics, and then make use of these characteristics together with compression algorithm, we can achieve a high compression rate and maintain a low CPU consumption.
An effective processing method is to sort the data before storing. There are often many dimension fields in the data table, such as region, date, etc. The values of these dimensions are basically within a small set range, and there will be many repeated values when the amount of data is large. If the data are sorted by these columns, it is common for adjacent records to have the same value. In this case, the use of a lightweight compression algorithm can obtain a good compression rate. To put it simply, we can directly store the column values and their number of repetitions, instead of storing the same values many times, this will save considerable space.
The order in sorting is also important, and we should put the column with longer field values in the first place as far as possible. For example, there are two columns: region and gender, and the number of characters of region values (“Beijing”, “Shanghai”, etc.) is greater than that of gender values ("male", "female"). In this case, the effect of sorting in the order of region and gender is better than that of sorting in reverse order.
In addition to sorting, we can also save the space by optimizing the data types, such as converting the string and date etc., to appropriate numeric code. If the region and gender fields are all converted to small integer numbers, the length of field values will be the same. After converting, we should put the field with more repeated values in the first place. For example, the gender has only two enumeration values, while the region has relatively more enumeration values, and hence there will be more repeated values in gender field. In this case, sorting by gender first and then region will usually occupy smaller space.
The columnar storage scheme provided in the open-source data computing engine SPL implements this compression algorithm. When the ordered data are appended to SPL’s composite table, SPL will automatically execute the above method by default, and only record the value once and number of repetitions.
SPL code for creating an ordered columnar storage composite table and performing the traversal calculation is roughly as follows:
Code example 1: Ordered and compressed columnar storage and traversal calculation
A |
|
1 |
=file("T_ordinary.ctx").open().cursor(f1,f2,f3,f4,…).sortx(f1,f2,f3) |
2 |
>file("T.ctx").create(#f1,#f2,#f3,f4,…).append@i(A1) |
3 |
=file("T.ctx").open().cursor().groups(…;sum(amt1),avg(amt2),max(amt3+amt4),…) |
A1: Create the cursor of the original data and sort by the three fields f1, f2, f3.
A2: Create a new composite table, and specify that the three fields f1,f2,f3 are ordered. Write the sorted data to composite table.
A3: Open the created new composite table, and perform the grouping and aggregating.
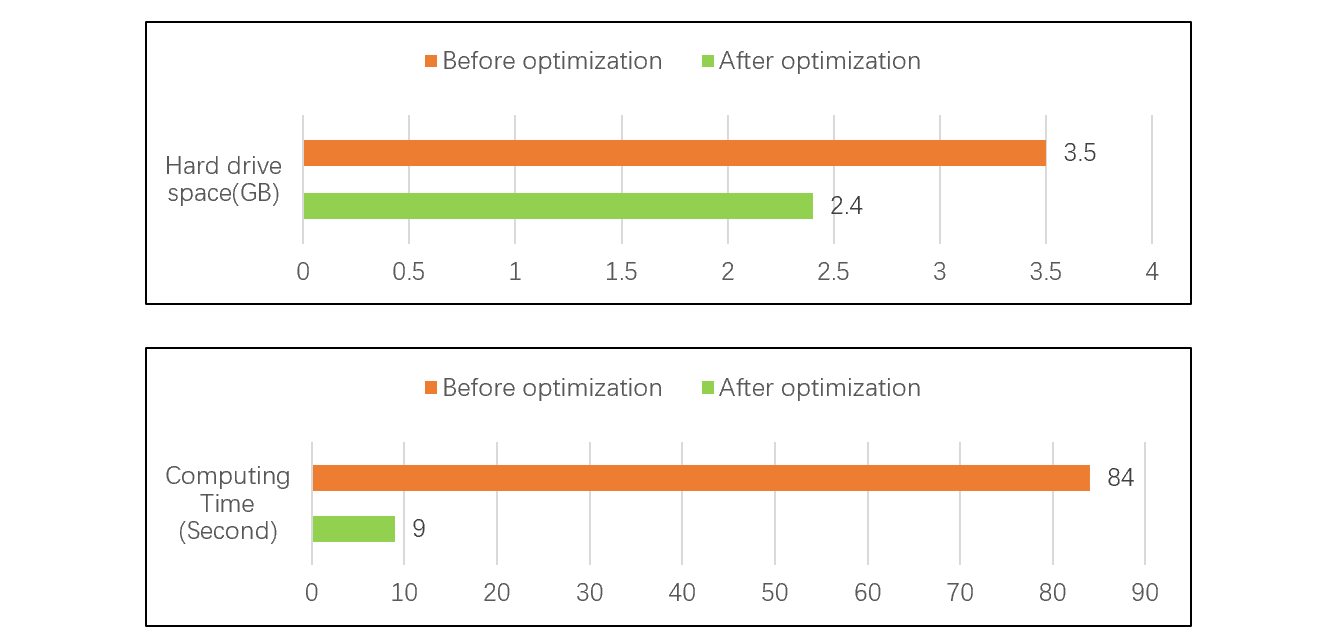
The following test shows that the data storage amount is reduced by 31% and the calculation performance is increased by more than 9 times after SPL adopts the data types optimization and the ordered and compressed columnar storage. See the figure for test results:
Parallel computing
Multi-thread parallel computing can make good use of the computing power of multiple CPUs, and is an important means to speed up. To perform parallel computing, the data need to be segmented first. For the row-based storage, the segmentation is relatively simple, that is, perform a rough average segmentation according to the amount of data, and then find the end mark of records to determine the position of the segmentation point. For the columnar storage, however, this method does not work. Since the different columns of columnar storage are stored separately, they must be segmented separately. In addition, because the lengths of fields are not fixed, and there are compressed data, the position of the same segmentation point of every column may not necessarily fall on the same record, which will lead to read error.
To cope with this problem, the industry generally adopts the blocking scheme to solve the segmentation synchronization of columnar storage: the data inside the block are stored as columnar storage; the segmentation must be performed in the unit of block; the parallel computing in segments is no longer performed inside blocks. To put this method into practice, it needs to first determine the size of data amount of each block. If the total data amount of data table is fixed, and no data are appended hereafter, it is easy to calculate the size of a suitable block. However, the data table will be appended continuously with new data in general, this will cause a contradiction on how to determine the size of the block. If the size of the block is determined to be large, the number of blocks will be relatively small when the total data amount is small at the initial stage, resulting in a failure in flexible segmentation, yet an even and flexible segmentation is the key to determine the performance of parallel computing. On the contrary, if the size of the block is determined to be small, the number of blocks will become large after the data amount increases, and the column data will be physically split into many discontinuous small blocks, this will cause an additional reading of a small amount of useless data in between blocks. Considering the seek time of hard disk, the more the number of blocks, the more serious the problem will be. Since many data warehouses or big data platforms cannot solve the contradiction between the size and number of blocks, it is difficult to make full use of parallel computing to improve performance.
SPL provides the double increment segmentation scheme, that is, change the fixed (physical) blocking into dynamic (logical) blocking. Through this scheme, the said contradiction can be well solved. The specific steps are : i)create an index area with fixed size (such as 1024 index units) for each column of data, and each index unit stores the starting position of one record, which means that one record represents one block; ii)append the data until all the index units are filled; iii) rewrite the index area, discard the even index units, and move the odd index units forward so as to empty the last half of index area, this step is equivalent to reducing the number of blocks to 512, and two records represent one block; iv)repeat the process of appending data, filling the index units, and rewriting the index area. With the increase of data amount, the size of blocks (number of records in a block) will be doubled continuously. It should be noted that the index areas of all columns should be filled synchronously, and the index areas should be rewritten synchronously after the index units are filled to keep them consistent. This scheme essentially uses the number of records as the segmentation basis, rather than the number of bytes, so it can ensure that the segmentation of every column is performed synchronously even if it is segmented separately, and there will be no misalignment.
When segmenting in the unit of dynamic block, the number of blocks is kept between 512 and 1024 (except when the number of records is less than 512), which can meet the requirement of flexible segmentation. Since the number of records corresponding to the dynamic block of each column is exactly the same, it can also meet the requirement of even segmentation. Therefore, a good segmentation effect can be obtained regardless of the amount of data. The detailed introduction to the principle of double increment segmentation can be found at: .
The composite table T generated in code example 1 adopts the double increment segmentation scheme by default. To do parallel computing on T, simply modify the code in A3 to:
=file("T.ctx").open().cursor@m().groups(…;sum(amt1),avg(amt2),max(amt3+amt4),…)
Parallel computing can be performed just by suffixing the option @m to the function cursor.
When appending data in the future, there is no need to regenerate the composite table, but open this composite table and append the data directly. The code is roughly like this:
> file("T.ctx").open().append@i(cs)
In this code, it needs to ensure that the to-be-appended data in the cursor cs are also ordered by the three fields f1, f2, f3. In practice, however, the to-be-appended may not meet this condition. To solve this problem, SPL provides a high-performance solution, visit: here for details.
Search
Columnar storage is more suitable for traversal calculation, such as grouping and aggregating. But for most searching tasks, columnar storage will lead to worse performance. When the index is not used, the usual columnar storage cannot use the binary search even if the data have been stored orderly. The reason is the same as parallel segmentation described above, it is still because that the columnar storage cannot ensure the synchronization of all columns, which may cause misalignment, thereby resulting in read error. In this case, the columnar storage data can only be searched by traversing, and the performance will be very poor.
To avoid transversal, we can create an index on the columnar storage data table, but it is very troublesome. Theoretically, if we want to record the physical positions of each field in the index, the index size will be much larger than the index of row-based storage, and may even be as large as the original data table (because each field has one physical position, and the amount of data in the index is the same as original data, and only the data type is simpler). Moreover, it needs to read the data respectively in the data area of each field when reading, yet the hard disk has a minimum reading unit, this will cause the total reading amount of each column to far exceed that of row-based storage, and the result is that the search performance is much worse.
Having adopted the double increment segmentation mechanism, SPL can more quickly find each field value in columnar storage according to record’s sequence number, which allows the binary search to be executed. Furthermore, since we only need to store the sequence number of the whole record into the index, the size of index will be much smaller and has little difference from the row-based storage. However, when using the binary search or index to search, it still needs to read the data blocks of each field respectively, and the performance still cannot catch up with row-based storage. Therefore, if you want to pursue an extreme search performance, you have to use row-based storage. In practice, it is preferably to let the programmer choose whether or not to adopt the columnar storage according to the needs of calculation. It’s a pity that some data warehouse products adopt the transparent mechanism that does not allow users to have their own choice on using the row-based storage or columnar storage, so it is difficult to achieve a best result.
SPL leaves this choice right to developers, who can decide whether to use the columnar storage and which data to use columnar storage according to actual needs, so as to obtain extreme performance.
In the introduction earlier, the composite table uses columnar storage by default, and also provides row-based storage mode, which can be specified using the option @r.
The code in A2 of code example 1 can be changed to:
=file("T_r.ctx").create@r(#f1,#f2,#f3,f4,…).append@i(A1)
This will generate a row-based storage composite table. With the two composite tables of columnar storage and row-based storage, programmers can freely choose and use them according to their needs.
For scenarios that require high performance for both traversal and searching, we can only trade storage space for calculation time. That is, store the data twice redundantly, and use the columnar storage for traversal, and use the row-based storage for search. However, since the data in such coexistence scheme need to be stored twice, and the index also needs to be created for row-based storage, the overall hard disk space occupied will be relatively large.
SPL also provides a “index with values” mechanism. When creating the index, other field values can be copied at the same time. The original composite table continues to use columnar storage for traversal, while since the index itself has stored field values and used row-based storage, the original table is generally no longer accessed during search, which can obtain better performance. Like the said coexistence scheme, this mechanism can give consideration to both the performances of traversal and search. Moreover, this mechanism combines the row-based storage with the index, and hence it occupies less space than the coexistence scheme.
Code example 2: Index with values
A |
|
1 |
=file("T.ctx").open() |
2 |
=A1.index(IDS;f1;f4,amt1,amt2) |
3 |
=A1.icursor(f1,f4;f1==123456).fetch() |
4 |
=A1.icursor(f4,amt2;f1>=123456 && f2<=654321) |
When creating the index IDS in A2, copying the to-be-referenced fields f4,amt1,amt2 into the parameter can duplicate these field values in the index. When the target values are fetched in the future, there is no need to read the original table as long as the involved fields are in the index.
Review and summary
When the columnar storage is used, it only needs to read the desired columns. When the total number of columns is large and the number of columns involved in the calculation is small, this storage method can reduce the access amount to hard disk and improve the performance. Yet, using columnar storage alone cannot reach our expectation, and for the columnar storage data warehouse, it also needs to optimize in data compression, multi-thread parallel computing and search calculation to maximize the effect of columnar storage.
The open-source data computing engine SPL makes full use of the feature of storing the data in an ordered way, and implements a compression algorithm with higher compression rate under the premise of keeping low CPU consumption, and greatly reduces the physical storage amount and further improves the performance. SPL also provides the double increment segmentation mechanism, which solves the problem of columnar storage segmentation, allowing the columnar storage data to fully use the parallel computing to improve efficiency. In addition, SPL can freely establish row-based storage and columnar storage data tables, allowing the developers to choose by themselves. What’s more, SPL provides the index-with-values mechanism, which can implement high performance traversal and search calculations at the same time.
SPL Official Website 👉 http://www.scudata.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProc
SPL Learning Material 👉 http://c.scudata.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/ydhVnFH9
Youtube 👉 https://www.youtube.com/@esProc_SPL



Chinese version