msum(A, n): calculate sum on a matrix or a multidimensional matrix,n is the dimensionalitylayeron which the summarization is performed.

For example a 5-by-4 matrix [[1,0,2,3],[0,71,5,6],[0,0,6,5],[35,53,2,3],[35,8,4,2]] can be summed on rows or columns by setting n

A1 Input the 5-by-4 matrix, with 5 vector members

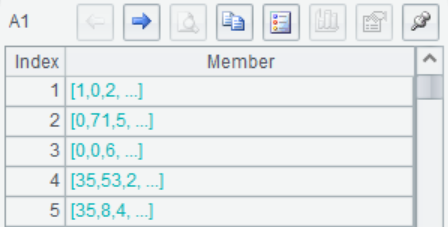
A2 n=1, calculate sum on the matrix’s first dimension layer, counterpoint addition of the vector members.That is, calculate sum on members of each column.

A3 n=2, calculate sum on the matrix’s seconddimension layer, add the elements within each vector. That is, calculate sum on members of each row.

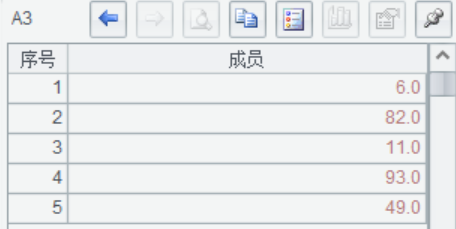
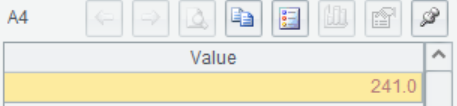
A4 @a means sum over all the elements of A1

Another example, in a 3-dimensional matrix, you can also sum in different dimensionlayer by setting n

A1 Inputa 3-dimensional matrix with 2 members, both 3-by-3 matrices

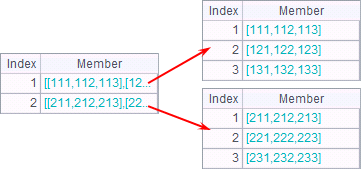
A2 n=1, the sum is summarized on the first dimension layer. That is, the counterpoint addition of two member matrices

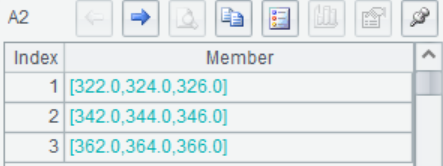
A3 n=2, the sum is summarized on the second dimension layer. That is, the counterpoint addition of three vectors in each member matrix

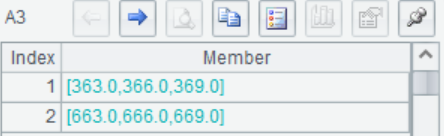
A4 n=3, the sum is summarized on the third dimension layer. That is, sum the members of each vector.

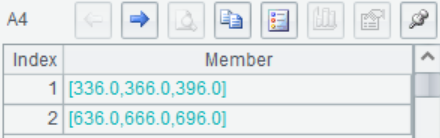
A5 @a means sum over all the elements of A1.