In parameter estimation and hypothesis testing, it is often necessary to construct distribution functions. The inverse cumulative distribution function (ICDF) of common distributions is provided in SPL. The ICDF functions in SPL are: norminv(), tinv(), chi2inv(), finv(), representing the normal distribution, T distribution, Chi square distribution, and F distribution respectively.

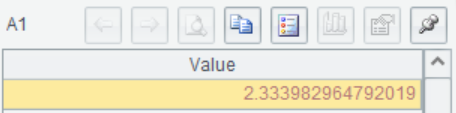
For example, the life of a group of products follows a normal distribution, mean mu=4, standard deviation sigma=1.3, the unit is years, calculate the time required for 10% of the product failure

	A
1	=norminv(0.1,4,1.3)

A1 Using the inverse normal cumulative distribution function, input the probability value, mean and standard deviation, and returns 2.334, that is, the time required for 10% product failure is 2.334 years

The inverse cumulative distribution function can also be used for interval estimation

For example, a golden sphere is used to determine the gravitational constant(unit: 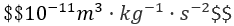), the observed values are 6.683，6.681，6.676，6.678，6.679，6.672

Assume the total measurement is 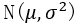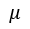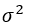，, both unknown, solve the confidence interval with a confidence=0.9 of 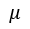, and solve the confidence interval with a confidence=0.9 of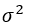

When 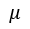, 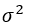both unknown, the confidence interval formula of 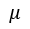is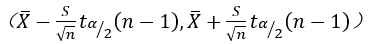

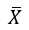is the sample mean, S is the sample standard deviation, and n is the sample size

In this case 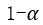=0.9, n=6

SPL code for interval estimates of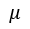

	A	B	C
1	[6.683,6.681,6.676,6.678,6.679,6.672]	0.9	6
2	=tinv(1-(1-B1)/2,C1-1)
3	=sqrt(var@s(A1))/sqrt(C1)*A2
4	=avg(A1)
5	=[A4-A3,A4+A3]

A1 Input the sample data

B1 Input the confidence is 0.9 which equals to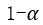

C1 Input the sample size n=6

A2 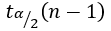is computed by using the T-distribution inverse cumulative function tinv(p, nu). p stands for cumulative probability and nu stands for degree of freedom, that is 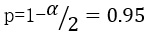, nu=n-1=5

A3 Calculate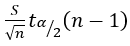

A4 Calculate the sample mean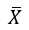

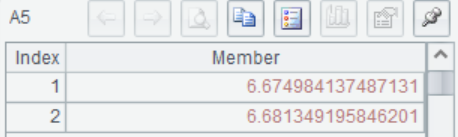
A5 Calculate the confidence interval. According to the return value we can get the confidence interval is （6.675，6.681）with confidence=0.9 of population mean

Similarly, the confidence interval of variance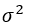 is 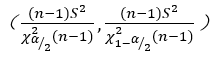, 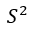means the sample variance

SPL code for interval estimates of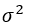

	A	B	C
1	[6.683,6.681,6.676,6.678,6.679,6.672]	0.9	6
2	=var@s(A1)
3	=chi2inv(1-(1-B1)/2,C1-1)
4	=chi2inv((1-B1)/2,C1-1)
5	=[(C1-1)*A2/A3,(C1-1)*A2/A4]

A1 Input the sample data

B1 Input the confidence is 0.9 which equals to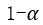

C1 Input the sample size n=6

A2 Calculated the sample variance

A3 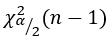is computed by using the Chi-square distribution inverse cumulative function chi2inv(p, v). p stands for cumulative probability and v stands for degree of freedom, that is 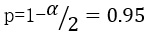, nu=n-1=5

A4 Calculate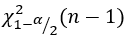

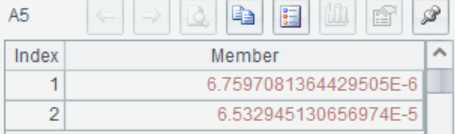
A5 Calculate the confidence interval. According to the return value we can get the confidence interval is 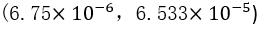with confidence=0.9 of population variance