The essay analyzes the fundamental reason behind slow SQL statements and provides the solution to make improvements through code samples. Looking SQL Performance Enhancement: TopN and Intra-group TopN for details.

Problem description

Getting TopN is to search for the max/min N records or values from data. Take Oracle for example, the SQL statement of doing this is as follows:

select * from (select x from T order by x desc) where rownum<=N

According to the statement, SQL sorts all data by x field and gets the top N records. Test shows that Oracle is able to automatically optimize the computation of getting TopN from the full data set by avoiding full-table sorting. The performance is satisfactory. Yet issues exist. For the more complicated scenario of getting TopN from each group after a grouping operation, it is hard for the database to do optimization.

To get intra-group TopN, Oracle has the following code:

select * from
    (select y,x,
        row_number()over (partition by y order by x desc) rn
    from T)
where rn<=N

SQL cannot directly code the computation. It calculates the sequence numbers in each group using the window function and then get the desired records. If a database does not support window functions, it is near-impossible to write a SQL statement for getting TopN from each group.

According to our test, Oracles calculates intra-group TopN n times slower than it gets TopN from a full data set. It is probably sorting has been performed. Yet the auto-optimization engine fails in the more complicated scenario.

The sorting-based TopN calculation is so slow because the algorithm is complex and time-consuming. The degree of complexity for sorting a number of (M) members is Mlog₂M and data will be traversed log₂M times. When the size of the source data is too large to be fit into the memory, the external buffering is resorted and computing speed drops sharply. Moreover, a large-scale sorting is difficult to be parallel processed.

Solution

To avoid the full-table sorting in getting TopN, we can keep a small set whose size is N for storing the temporary TopN during the traversal. If the current item is greater than the Nth item in the set, insert it into the set and discard the Nth item. If the current one is smaller than the Nth item, just keep the set unchanged.

Only one traversal is needed. And generally, the N-size set is small enough to fit into the memory. Even if the total volume of data involved is large, data exchange between memory and external memory won’t happen. Actually, as the new algorithm does not need a sorting, it will increase the performance of getting TopN if the computation involves a not very large volume of data that can fit into the memory.

The complexity degree of getting TopN from M members using the new algorithm is Mlog₂N. If N<<M, the new algorithm is far simpler than the sorting-based algorithm. It is also easy to perform the segmentation-based parallel processing with the algorithm. We just need to get TopN from each segment, union the TopNs, and get the final TopN. The concurrent write on the hard disk won’t happen.

The new algorithm, in essence, treats getting TopN as a type of aggregate operation. The aggregate we are familiar with, like sum, count, max and min, handles a set to get a single value. TopN, however, returns a small-scale result set. By considering it as aggregation, it can be dealt with using methods of getting aggregates. We handle post-grouping intra-group TopN computation in the same way as we handle post-grouping sum, count, max and min operations. The computation becomes easy when no sorting operation is needed.

Sample code

Ⅰ. Getting TopN from a full data set

A1: Open the composite table.

A2: Create a 4-thread multicursor. The total()function performs aggregation on the whole data set. top(-5,x) gets Top5 records where x field value is the largest, and top(5,x) gets Top5 records where x field value is the smallest.

A2 Below is the final result:

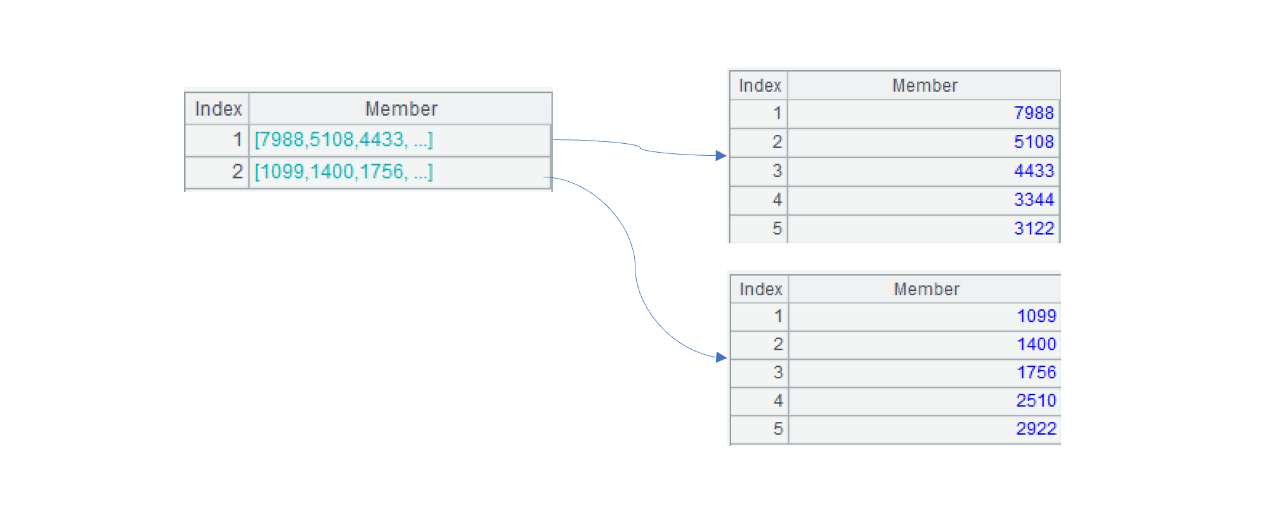
We can see that the largest 5 and the smallest 5 are two sets.

Ⅱ. Getting intra-group TopN

A2: groups(y;top(-3,x), top(3,x) groups data by y field and calculates the largest 3 and smallest 3 separately in each group. As the cursor function does not explicitly define the number of parallel threads through a parameter, it generates a multicursor automatically according to the maximum number of parallel threads in the system configurations. We can use top(-3,x):top3 to rename fields in the result set.

A2 Below is the final result:

The result set has three fields. The first field is the grouping field. The second field is the set of the largest 3. The third field is the set of the smallest 3.